Constará de tres preguntas, a elegir entre dos. La calificación máxima de esta parte de preguntas de desarrollo es de 5 puntos (2,5 puntos por pregunta).
Problemas de desarrollo
1. Representar la región dada por las siguientes inecuaciones.
a) Halla los puntos de la región factible en los cuales estarían los posibles extremos de una función cualquiera.
\begin{cases} 2x + 2y \leq 6 \\ x \geq 2 \\ 3x - 6y \geq 0 \\ x \geq 0 \\ y \geq 0 \end{cases}
b) Sabiendo que la función z=3x+5y representa el número de periodos y el conjunto de inecuaciones anteriores son las condiciones, calcular si es posible, el número máximo y mínimo de periodos que se pueden realizar.
2. Un club deportivo va a presentarse a una competición en la que se clasificará para la siguiente fase si la puntuación media obtenida por los deportistas es superior a 24 puntos. La distribución de los puntos obtenidos por los equipos sigue una distribución normal de media 25 con una desviación típica de 5 puntos. ¿Qué probabilidad de clasificarse tiene el club si se presenta un equipo formado por 15 deportistas? ¿Y si el equipo lo forman 25 deportistas? ¿Qué equipo será seleccionado para participar?
3. Determinar el valor de K y de q para que la función sea continua en todos los puntos.
Soluciones
Problema 1
a)
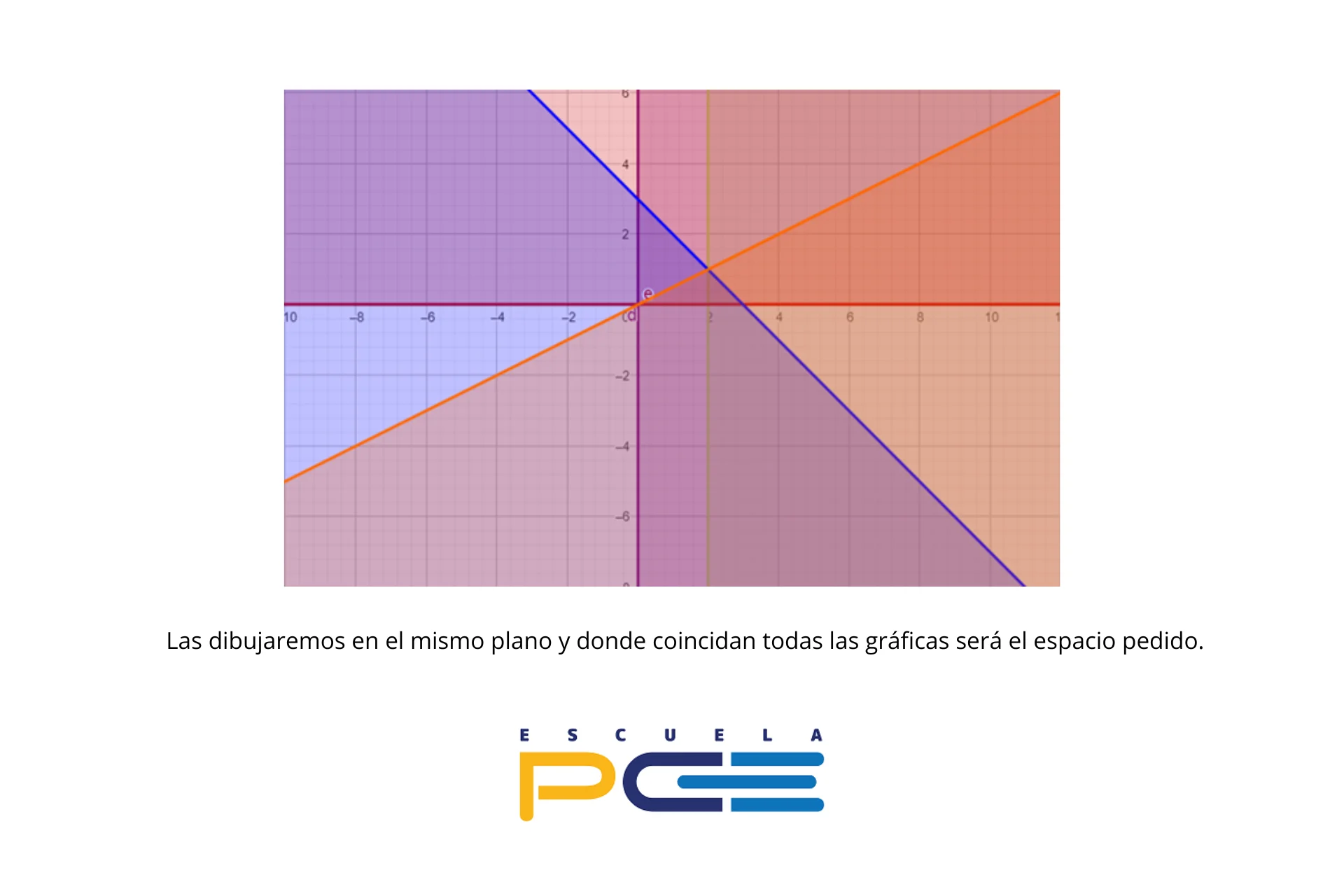
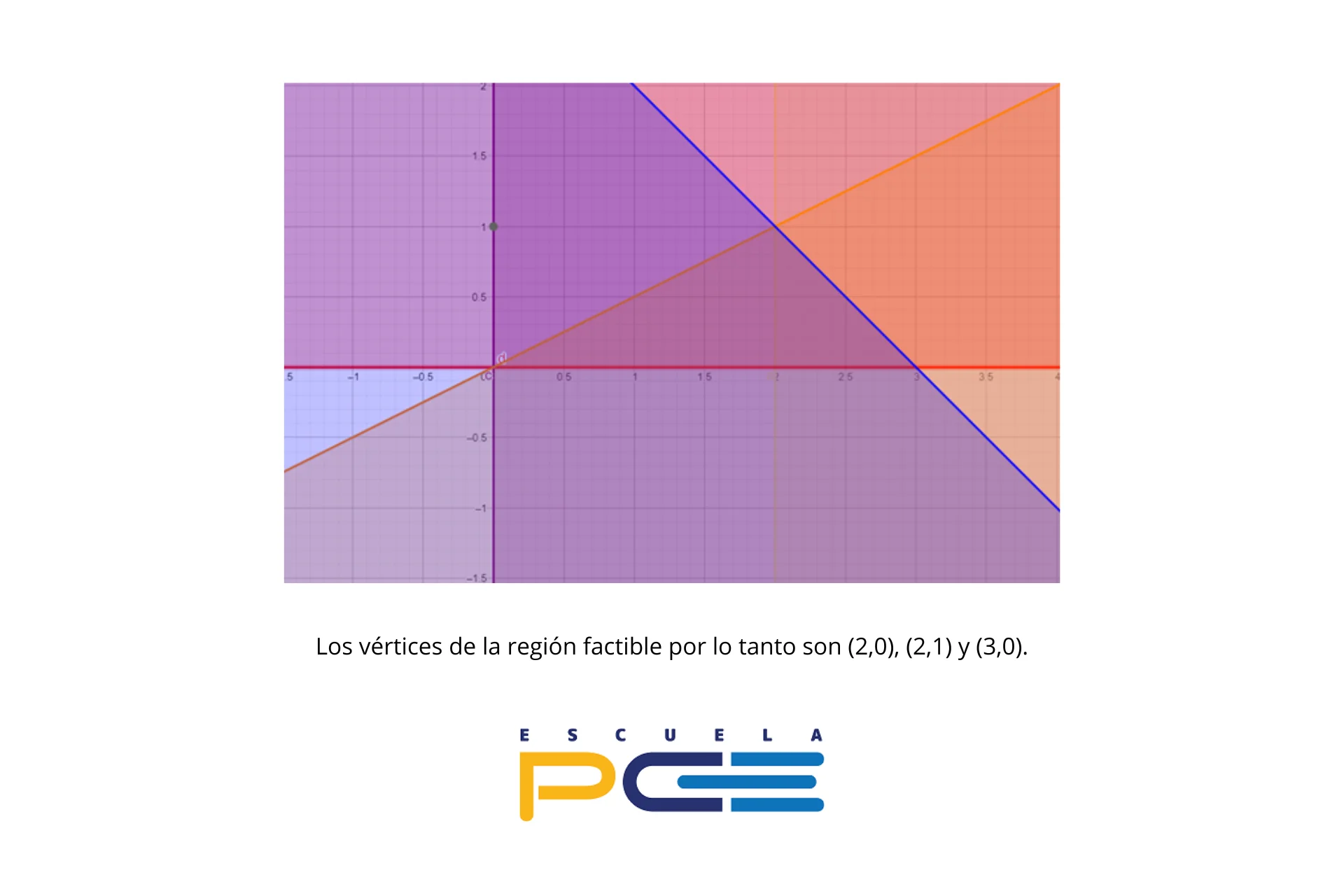
b) Como la función objetivo ya nos la dan que es z=3x+5y, lo que tendremos que hacer es utilizar los vértices anteriores para obtener los posibles máximos y mínimos.
(2,0) –> Z(2,0)= 6
(3,0) –> Z(3,0)= 9
(2,1) –> Z(2,1)=11
Por lo que tenemos que el máximo número de pedidos será de 11 y el mínimo de 6.
Problema 2
Los parámetros importantes que obtenemos del enunciado son:
{x} = 24 \quad \sigma = 5 \quad \mu = 25
a) Para n=15, al estar en una media muestral tendremos N\left(25, \frac{5}{\sqrt{15}}\right).
Al pedirnos P(\bar{x} > 24) tendremos que pasarlo Z , por lo que Z=\frac{\bar{x} -\mu}{\sigma}, sustituyendo tenemos que Z = -0,7746
Por lo que:
P(Z > -0,7746) = P(Z < 0,7746). Buscando en la tabla encontramos que (P(Z<0,7746) = 0,7794
b) Para n=25, haciendo el mismo paso que antes N(25,1), entonces (P(Z>-1)). Por lo que (P(Z<1) = 0,8413)
c) Por lo que el equipo seleccionado será el de 25 jugadores.
Problema 3
f(x) = \begin{cases} x^2 & x \in (-\infty, 2] \\ 2kx & x \in (2,4) \\ q + x & x \in (4, +\infty) \end{cases}
Para que una función sea continua es necesario que se cumpla: �(�)=lim�→�−�(�)=lim�→�+�(�)f(a)=limx→a−f(x)=limx→a+f(x). Es importante recordar que los corchetes indican que está incluido dentro del intervalo. Estudiaremos por partes los límites:
Para x=2
f(2) = x^2 = 4\\lim_{{x \to 2^+}} 2kx = 4k \\ \lim_{{x \to 2^-}} x^2 = 4Como tienen que ser iguales, entonces K=1
Para x=4
f(4) = 2kx = 8 \quad \text{usando } k = 1 \Rightarrow 8 \times 1 = 8 \\lim_{{x \to 4^+}} (q + x) = q + 4 \quad \text{Para que sea continua debe ser igual a } 8 \Rightarrow q = 4 \\lim_{{x \to 4^-}} 2kx = 8Por lo que el valor debe ser q=4 y k=1.




